
So that you will not be easily deceived by what you see, it is worth going over why large aircraft appear to fly slower than small aircraft.
If we consider a class of aircraft of similar geometry and construction (for example, balsa and MonoKote or fiberglass and foam), the weight will scale as the cube of a characteristic length. This follows generally from mass being equal to density times volume. Taking the wing span as the characteristic length, we can therefore write:

Likewise for the wing area we have

These relations together form what is often called the "square-cube law," from which a wealth of useful information may be derived. For instance, these equations can be combined to give
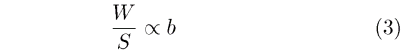
Thus if a model is scaled up to twice its size, the wing loading will double if the construction materials are similar. This relationship can be used to estimate the weight of new designs based on old ones. It is only necessary to determine the proportionality constant. Also, from the equation for lift
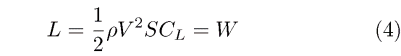
we can obtain
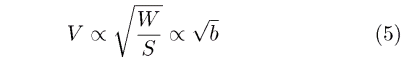
This shows that if we increase the span and keep geometrically similar models with the same type of construction, then the speed at a given lift coefficient will increase with the square root of the wing span. It does not yet show why large aircraft look slower than small aircraft.
When an aircraft is flying against a blue sky, the only relative measure of length or size is the aircraft itself. Therefore, we can only base the speed on how long it takes the aircraft to cover some characteristic distance relative to its own size. If we take the wing span as this characteristic distance and call the time that it takes the aircraft to travel one wing span the "characteristic time," then we can write it as
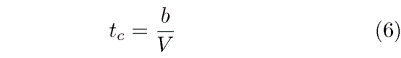
From (4) we can than then write

Immediately we see that as the span increases so too does the time it takes to travel a distance of one wing span.
Finally, we can compare the "speeds" of a 2M and XC sailplane by forming the ratio
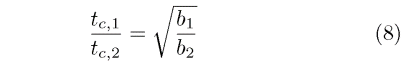
If the wing span of the larger plane (denoted as 1) is twice the smaller
(2), then the time it takes the larger plane to travel one wing span is
41% longer than the smaller. Although it is actually flying 41% faster
(see equation (5)), it looks 41% slower. That is a big difference.
RC Soaring Digest on-line articles